Wormholes and cryptocurrencies appear completely unrelated. However, as is thankfully often the case, unexpected connections lie beneath the surface. Indeed, there is a conceptual bridge between wormholes—bridges in spacetime—and blockchains, the technology that underpins crypto such as Bitcoin. It is a connection, recently proposed by Alexey Milekhin, that involves a journey through general relativity, quantum mechanics, and blockchains, ending with an emergence view of time.
What I am presenting here is not a novel discovery; rather, it represents a fresh perspective grounded in findings aligned with Gerard ‘t Hooft’s holographic principle. This principle posits that the entropy of mass is proportional to surface area rather than volume, implying that volume is illusory, and the universe is essentially a hologram mirroring the information encoded on its boundary. This insight takes on a new dimension when applied to wormholes, revealing that time itself is an emergent phenomenon rooted in “quantum circuit complexity.” Moreover, the logical framework of blockchain technology offers a tangible model of this emergent time.
Wormholes
To delve into the depths of this concept, one must first comprehend what wormholes are. Wormholes are extraordinary solutions to Einstein’s field equations, bridging distant points in spacetime by forming tunnels connecting different locations, times, or both. A quintessential example of a wormhole is the Einstein-Rosen (ER) bridge, an extension of the Schwarzschild metric that unites two universes through a two-sided, spherically symmetric, and chargeless black hole. What makes this bridge special is its requirement for spacetime to have no “edges,” allowing a free-falling particle’s trajectory to extend infinitely into the past and future, even within the gravitational pull of a black hole. For this to occur, the interior of an ER bridge must host both a region where particles fall in (the black hole interior) and another region where particles escape (the white hole interior), along with two separate exterior regions.
Two crucial facts emerge from the interior—the tunnel—of a wormhole: its volume linearly increases with time and it saturates at a volume of Exp(S0), where S0 is the leading order entropy of the black hole which has been determined by Bekenstein and Hawking to be a quarter of the horizon area. The fact that the entropy of a black hole is determined by the horizon’s area can be seen as corroborating evidence for the holographic principle. As a cool sidenote, it is widely believed that canonical ways of quantisation fail to work with gravity due to the holographic principle. Quantising gravity as a local field theory implies that local fluctuations over the entire volume of spacetime act as degrees of freedom, however according to the holographic principle the entropy and thus the true degrees of freedom are on the “boundary” and not in the “volume”. The effect, simply due to volume inherently having more dimensions than the boundary, is a massive overcounting which makes the theory not renormalisable, or in simpler words, infinities are introduced in the theory which one cannot get rid of.
“Complexity=Time” conjecture
The two intriguing facts about the volume of the interior of a wormhole are not just important due to the holographic principle, they also illustrate that volume behaves suspiciously similar to what is known as the “quantum circuit complexity of state preparation” near the horizon of a wormhole. Near the horizon, according to quantum field theory, there is an energy divergence due to rising local temperatures—a consequence of substantial gravitational acceleration, known as the Unruh effect. This divergence can be reconciled by a theory for which the effective degrees of freedom go to zero near the horizon, since then finite energy at the horizon can be achieved due to how heat, temperature, and entropy are related by Clausius’ theorem. This involves placing all the degrees of freedom on a membrane situated just a Planck length away from the horizon. These degrees of freedom can then be modelled as thermalised, non-localised qubits—two-level quantum systems encoding information—living on the membrane. Information entering the horizon generates local perturbations on this membrane, which eventually diffuse and restore thermal equilibrium. During this thermal process, the qubits of the membrane naturally get scrambled up. The scrambling process is more precisely a quantum evolution process, and thus can be described by a specific Hamiltonian. This is called a k-local Hamiltonian, and it acts on the qubits at each time step by grouping k qubits and making them interact through a random quantum logic gate, a random generalised Pauli matrix. Over time, this sequence of quantum logic gates begins to form an increasingly complex quantum circuit. The complexity of a quantum circuit actually has a rigorous definition: given an initial and a final quantum state related via a unitary operator U, and a set of allowed quantum gates, the quantum complexity is the minimum number of quantum gates it takes to construct U. The crux of the matter can now be arrived at: quantum complexity linearly increases with time, and by a combinatorial argument it can be easily shown that it saturates to an exponential in the number of qubits (also known as the degrees of freedom, characterised by S0).
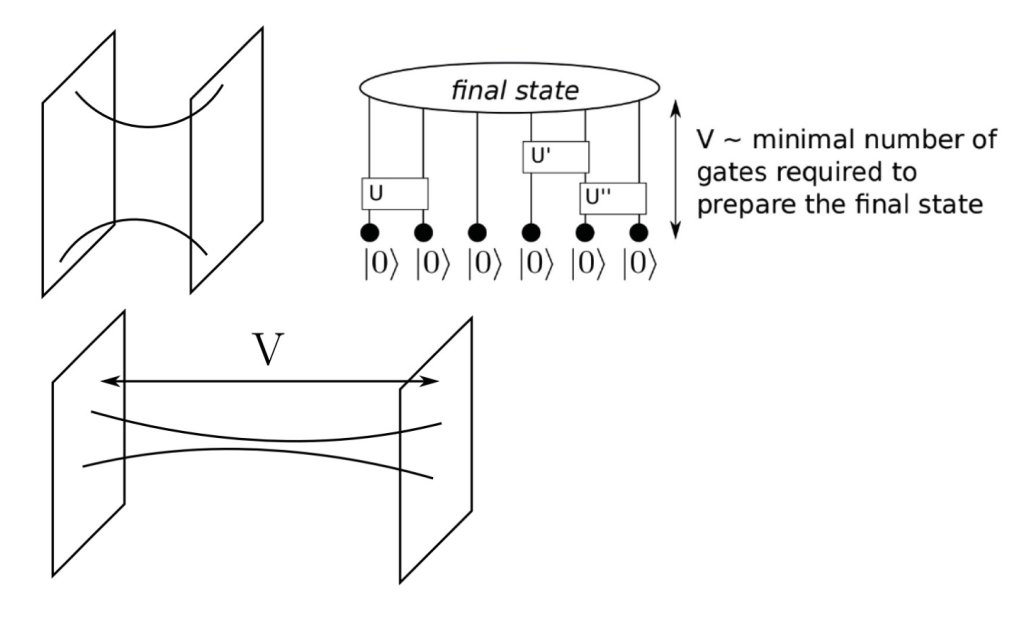
Let all this sink in, and notice that these two facts about quantum complexity at the horizon of a wormhole are suspiciously similar to the two facts about the volume of the interior of a wormhole! This similarity has prompted physicists to argue for the “Complexity=Volume” conjecture: the volume of a wormhole is equal to the quantum complexity of state preparation at its horizon. But, due to the extreme curvatures in spacetime involved here, what is a space coordinate within the horizon, is a time coordinate outside. Hence, more generally, outside wormholes, we can infer from the “Complexity=Volume” conjecture a new “Complexity=Time” conjecture. This “Complexity=Time” conjecture, a conjecture consistent with both quantum mechanics and general relativity, sheds a profound light on the origins of time itself. It suggests that time, which we perceive as a continuous and fundamental aspect of our experience, emerges from the intricate dance of an ever-increasing complexity. Time is no longer a pre-existing concept but rather a product of information processing and the fundamental properties of quantum states.
Blockchain
While the concept of “Complexity=Time” may initially appear elusive, and concrete physical examples may not be readily apparent, an intriguing parallel in blockchain technology adds a layer of tangibility. The blockchain protocol, which serves as the cornerstone of cryptocurrencies and various other applications, in fact exhibits the emergence of time and it is inherently defined by the “Complexity=Time” principle.
The blockchain concept was introduced by Satoshi Nakamoto in his 2008 paper, titled “Bitcoin: A Peer-to-Peer Electronic Cash System”. This revolutionary innovation aimed to provide a reliable digital alternative to traditional cash, allowing secure transactions between parties without relying on centralised financial institutions. However, at its core, a blockchain is a decentralised and distributed digital ledger that records a chronological and immutable series of data entries. It is an elegant solution to the following problem: how can we establish an emergent universally agreed-upon global time, a chronology that harmonises the messages exchanged among N observers? This task requires arranging messages into a linear structure, akin to a chain of blocks. Unlike conventional timestamping, which relies on synchronised clocks—a notorious issue exacerbated by the theory of relativity—blockchain avoids this complexity and potential for errors or desynchronization. It does so by first ensuring, through advanced cryptographic algorithms, that attaching a genuine new block—a new message, a new financial transaction—next to a previous block in the chain must be very computationally expensive, whereas verifying the validity of a block must be very easy. Yet, this alone does not resolve the consensus problem, because the chain could potentially branch into different and contradictory timelines. The full solution comes into play by combining the computational imbalance principle with Nakamoto’s principle: “The longest chain is the correct one”. In this context, “longest” is synonymous with “the most complex”, given that each block carries roughly the same computational complexity. Therefore, when an observer intends to append a block, they should do so on the longest chain. If they deviate from the longest chain in an attempt to alter history to their advantage, they end up working alone, engaging in a computationally expensive process to create new blocks. Meanwhile, the rest of the network cooperatively secures the main branch, ensuring its correctness. This dynamic leads to the continuous growth of complexity within the blockchain, ultimately giving rise to a global time concept, just like in the “Complexity=Time” conjecture! In fact, correct chains maximising complexity in the blockchain is completely analogous to Lorentzian time-like geodesics maximising the proper distance in spacetime.

What’s truly remarkable is that within the realm of blockchain technology, not only does the emergence of consensus on time become evident, but also the potential for consensus in other domains of paramount importance. From research and science to law, ethics, and even innovative forms of governance such as Decentralized Autonomous Organizations (DAOs) and algocracy, blockchain’s inherent principles lay the foundation for a global consensus. These breakthroughs exemplify that beyond reshaping the fundamental nature of time, blockchain may hold the key to fostering consensus in an array of critical domains pertaining to the human condition. To go even further, consider that is has been speculated that we live in a simulation. Perhaps we live in a blockchain!